Answer:
Third option: x=0 and x=16
Explanation:
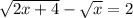
Isolating √(2x+4): Addind √x both sides of the equation:
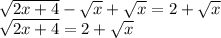
Squaring both sides of the equation:
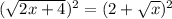
Simplifying on the left side, and applying on the right side the formula:
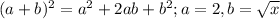
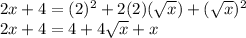
Isolating the term with √x on the right side of the equation: Subtracting 4 and x from both sides of the equation:
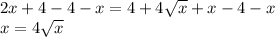
Squaring both sides of the equation:
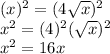
This is a quadratic equation. Equaling to zero: Subtract 16x from both sides of the equation:
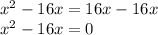
Factoring: Common factor x:
x (x-16)=0
Two solutions:
1) x=0
2) x-16=0
Solving for x: Adding 16 both sides of the equation:
x-16+16=0+16
x=16
Let's prove the solutions in the orignal equation:
1) x=0:
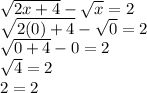
x=0 is a solution
2) x=16
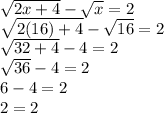
x=16 is a solution
Then the solutions are x=0 and x=16