Question

What is the solution of

Answer 1

Third option: x=0 and x=16

Explanation:

`√(2x+4)-√(x)=2`

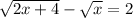
Isolating √(2x+4): Addind √x both sides of the equation:

`√(2x+4)-√(x)+√(x)=2+√(x)\\ √(2x+4)=2+√(x)`

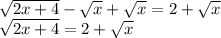
Squaring both sides of the equation:

`(√(2x+4))^(2)=(2+√(x))^(2)`

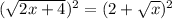
Simplifying on the left side, and applying on the right side the formula:

`(a+b)^(2)=a^(2)+2ab+b^(2); a=2, b=√(x)`

`2x+4=(2)^(2)+2(2)(√(x))+(√(x))^(2)\\ 2x+4=4+4√(x)+x`

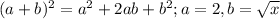
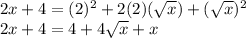
Isolating the term with √x on the right side of the equation: Subtracting 4 and x from both sides of the equation:

`2x+4-4-x=4+4√(x)+x-4-x\\ x=4√(x)`

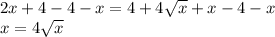
Squaring both sides of the equation:

`(x)^(2)=(4√(x))^(2)\\ x^(2)=(4)^(2)(√(x))^(2)\\ x^(2)=16 x`

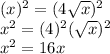
This is a quadratic equation. Equaling to zero: Subtract 16x from both sides of the equation:

`x^(2)-16x=16x-16x\\ x^(2)-16x=0`

Factoring: Common factor x:

x (x-16)=0

Two solutions:

1) x=0

2) x-16=0

Solving for x: Adding 16 both sides of the equation:

x-16+16=0+16

x=16

Let's prove the solutions in the orignal equation:

1) x=0:

`√(2x+4)-√(x)=2\\ √(2(0)+4)-√(0)=2\\ √(0+4)-0=2\\ √(4)=2\\ 2=2`

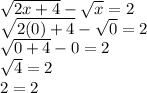
x=0 is a solution

2) x=16

`√(2x+4)-√(x)=2\\ √(2(16)+4)-√(16)=2\\ √(32+4)-4=2\\ √(36)-4=2\\ 6-4=2\\ 2=2`

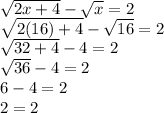
x=16 is a solution

Then the solutions are x=0 and x=16