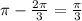Answer:
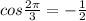 .
.
Reference angle is
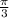
Explanation:
Given the value of x. we have to find the correct value of cosx.
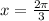
Now, we have to find the exact value of

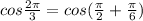

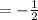
Now, we have to find the reference angle of
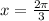 .
.
Since the angle
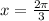 lies in second quadrant, the reference angle formula is
lies in second quadrant, the reference angle formula is
Reference angle=
 .
.
=