Question

If each term of an arithmetic sequence is multiplied by a fixed​ number, will the resulting sequence always be an arithmetic​ sequence?

Answer 1

yes correct, also when you are adding or subtracting

Explanation:

Answer 2

Yes, the resulting sequence will always be an arithmetic sequence.

Explanation:

We know that any arithmetic sequence is a sequence in which each term of the sequence is increased by a fixed constant as compared to the preceding term of the sequence.

This fixed constant is known as common difference,

i.e.
`d=a_n-a_(n-1)`

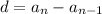
where

`a_n` is the nth term of the sequence.

Now, when each term of an arithmetic sequence is multiplied by a fixed​ number let a'.

Let
`a_n'` is the nth term of the new sequence.

Then we have:

`a_1'=a'a_1`

`a_2'=a'a_2`

`a_3'=a'a_3`

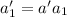
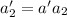
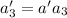
and so on

Also,

`a_(n)'-a_(n-1)'=a'a_n-a'a_(n-1)\\\\a_(n)'-a_(n-1)'=a'(a_n-a_(n-1))\\\\a_(n)'-a_(n-1)'=a'd`

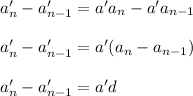
for each n.

Hence, the sequence will again be an arithmetic sequence.

( Since, the sequence again vary by a fixed constant )