Answer:
14- The given sequence has common ratio =
 , so it is a geometric sequence.
, so it is a geometric sequence.
15- explicit :
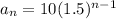 , recursive :
, recursive :

Explanation:
Ques 14: We have the sequence,
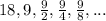 .
.
So, we will find the common ratio of the given sequence,
i.e. Common ratio =
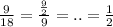
Thus, we have,
The given sequence has common ratio =
 , so it is a geometric sequence.
, so it is a geometric sequence.
Ques 15: We have the sequence,

As, the common ratio of the given sequence =
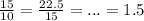
Thus, the explicit form is given by,
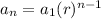 i.e.
i.e.
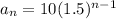 .
.
Also, the recursive form is given by,
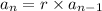 i.e.
i.e.
 .
.