Question

Select the correct answer.

What is the standard form of '((2+3i)(4-71))/((1-1)) ?
O A.
-3/13-4/261
OB.
*3/13+4/261
O c.
31/2+27/21
OD.
.-31/2-27/21
Plz halp

Answer 1

`(31)/(2)+(27)/(2)i`

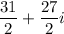
Explanation:

The given complex number is:

`z=((2+3i)(4-7i)(1+i))/((1^2-i^2))`

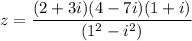
Firstly we can solve (2+3i)(4-7i)(1+i)

= 2(8)+2(-7i)+4(3i)+3i(-7i²)× (1+i)

= (16-14i+12i-21i²i)× (1+i)

Since, i² = -1

= (16-14i+12i-21(-1)i)× (1+i)

= (16-14i+12i+21)× (1+i)

= (29-2i)(1+i)

= 31+27i

Denominator : (1-i²)

= (1-(-1))

= 2

`((2+3i)(4-7i)(1+i))/((1^2-i^2))=(31+27i)/(2)\\\\=(31)/(2)+(27)/(2)i`

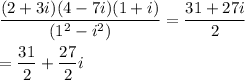
Hence, the correct answer is
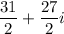`(31)/(2)+(27)/(2)i`.