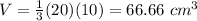Answer:
Figures C and D have the same volume
Explanation:
Part 1) Find the volume of Figure A
we know that
The volume of a cone is equal to
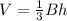
where
B is the area of the base
h is the height of the cone
In this problem we have
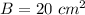
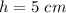
substitute
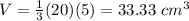
Part 2) Find the volume of Figure B
we know that
The volume of a cylinder is equal to
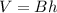
where
B is the area of the base
h is the height of the cylinder
In this problem we have
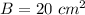
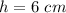
substitute
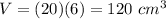
Part 3) Find the volume of Figure C
we know that
The volume of a cylinder is equal to
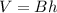
where
B is the area of the base
h is the height of the cylinder
In this problem we have
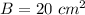
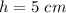
substitute
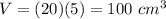
Part 4) Find the volume of Figure D
we know that
The volume of a rectangular prism is equal to
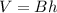
where
B is the area of the base
h is the height of the prism
In this problem we have
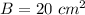
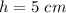
substitute
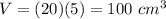
Part 5) Find the volume of Figure E
we know that
The volume of a pyramid is equal to
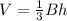
where
B is the area of the base
h is the height of the pyramid
In this problem we have
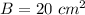
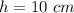
substitute