Question

W varies jointly as X and Y and inversely as the square of Z. If W=280 when X=30, Y=12, and Z=3, find W when X=20, Y=10, and Z=2.​

Answer 1

Hello! Its Me! :)

Answer:

The answer is 350.

Explanation:

The joint variation of W with x, y and z may be expressed as follow, W = kxy / z²where k is the constant of variation. Substituting the first set of values for the variables, 280 = k(30)(12) / 3²The value of k from the equation is 7. Substituting to the same equation the values of the next set of variables, w = (7)(20)(10) / 2² = 350

Answer 2

W = 350

Explanation:

W varies jointly as X and Y and inversely as the square of Z.

That means W ∝
`(XY)/(Z^(2) )`

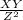
Or W =
`(kXY)/(Z^(2) )`

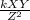
Where k is the proportionality constant.

Now as per statement we will plug in the values

W = 280, X = 30, Y = 12 and Z = 3 to find the value of constant k

280 =
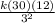
`(k(30)(12))/(3^(2) )`

k =
`(280* 9)/(360)`

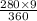
k = 7

Now we plug in the values

X = 20, Y = 10, Z = 2 and K = 7 to find the value of W.

W =
`(7* 20* 10)/(2^(2) )`

=
`(1400)/(4)`

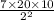
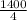
= 350

Therefore, W = 350 is the answer.