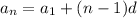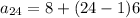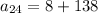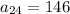Question

What is the 24th term if the arithmetic sequence where a1 = 8 and a9 = 56

Answer 1

`a_(24) = 146`

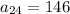
Explanation:

a1 = 8

a9 = 56

Using formula for finding nth term of arithmeric sequence

`a_(n) =a_(1) + (n-1)d`

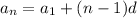
We have to find 24th term, therefore n = 24

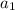`a_(1)` is the first term but we are missing d

d is the difference between the two consecutive terms, lets calculate it first

a9 = 56

Using the above given formula for finding d

put n = 9, a9= 56

`a_(9) =a_(1)+ (9-1)d`

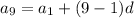
56 = 8 + 8d

8d = 48

d = 6

Getting back to main part of finding 24th term

n = 24, d = 6, a1 = 8

put values in nth term formula

`a_(n) =a_(1)+ (n-1)d`

`a_(24) = 8 + (24-1)6`

`a_(24) = 8 + 138`

`a_(24) = 146`