Answer:
Option D. 13122 is the answer.
Explanation:
As we can see from the table having interval and average rate of change, figures under average rate of change are forming a geometric sequence.
Sequence is 2, 6, 18 , 54, 162, 486.
and we have to find the average rate of change from x = 8 to x = 9, means we have to find 9th term of the given sequence.
Now we know that explicit formula of the sequence can be written as
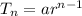
where Tn is the nth term of the sequence.
a = first term
r = common ratio
n = number of the term
Now from this explicit formula we can find the 9th term of the sequence.
From the given table
a = 2, r = 3, n = 9
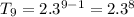
T9 = 13122
Therefore Option D. 13122 will be the answer.