Question

For f(x) = 4x + 1 and g(x) = x ^ 2 - 5 , find (f o g)(4)

Answer 1

Explanation:

(f o g)(x)

= f(x² - 5)

= 4(x² - 5) + 1

= 4x² - 19.

Therefore (f o g)(4) = 4(4)² - 19 = 64 - 19 = 45.

Answer 2

`\boxed {\boxed {\sf 45}}`

Explanation:

When solving a composition of function composition, work from the inside to the outside.

We have the composition:

• (f o g)(4)

We must start on the inside, and find g(4) first.

1. g(4)

The function for g is:

`g(x)=x^2-5`

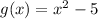
Since we want to find g(4), we have to substitute 4 in for x.

`g(4)=(4)^2-5`

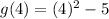
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Addition, and Subtraction. First we should solve the exponent.

• (4)²= 4*4= 16

`g(4)=16-5`

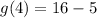
Subtract 5 from 16.

`g(4)= 11`

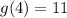
Now, since g(4) equals 11, we have:

• (f o g)(4)= f(11)

2. f(11)

The function for f is:

`f(x)= 4x+1`

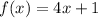
We want to find f(11), so substitute 11 in for x.

`f(11)= 4(11)+1`

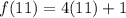
Solve according to PEMDAS and multiply first.

`f(11)= 44+1`

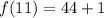
Add.

`f(11)= 45`

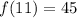
(f o g)(4) is equal to 45.