Answer:
The painting is 42.13 feet above the platform
Explanation:
Refer the attached figure .
A particular painting forming an angle of 50 degrees with a camera platform .
∠ABC = 50°
We are also given that the light is 55 feet from the wall where the painting hangs
i.e. AB = 55 feet.
Now we are required to find how high above the platform is the painting. i.e. AC
So, we will use trigonometric ratio :

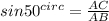
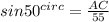
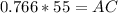
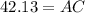
Thus the painting is 42.13 feet above the platform