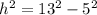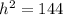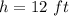Answer:
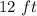
Explanation:
The question in English is
A 13-foot long staircase rests on a wall, so that the base of the staircase is separated from the wall, at floor level, at a distance of 5 feet. Calculate the height of the ladder on the wall. Remember that in a right triangle, the hypotenuse, squared, is equal to the sum of the squares on the other sides. If necessary, approach the tenth foot
Applying the Pythagoras Theorem
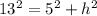
Solve for h