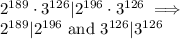Question

Prove the divisibility of the following numbers:

Question A

45^45·15^15 by 75^30

Question B

24^54·54^24·2^10 by 72^63

Question C

45^10·5^40 by 25^20

Question D

12^8·9^12 by 6^16

Answer 1

Explanation:

To prove divisibility, we need to factor the divident such that one of its factors matches the divisor.

(I use the notation x|y to denote that x divides y)

(A)

`75^(30)|45^(45)\cdot15^(15)\\45^(45)\cdot15^(15)=3^(45)\cdot 15^(45)\cdot 15^(15)=\\=3^(45)\cdot 15^(60)=3^(45)\cdot 15^(30)\cdot 15^(30)=3^(45)\cdot (3\cdot5)^(30)\cdot 15^(30)=\\=3^(45)\cdot 3^(30)\cdot(5\cdot 15)^(30)=3^(45)\cdot 3^(30)\cdot(75)^(30)\\\implies\\75^(30)|3^(45)\cdot 3^(30)\cdot75^(30)`

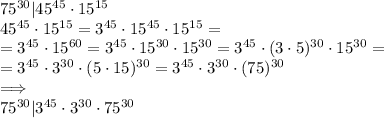
(B)

`72^(63)|24^(54)\cdot 54^(24)\cdot2^(10)\\24^(54)\cdot 54^(24)\cdot2^(10)=(2^(162)\cdot 3^(54))\cdot(2^(24)\cdot 3^(72)) \cdot 2^(10)\\=2^(196)\cdot 3^(126)`

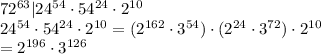
In this case, it is easier to also factor the divisor to primes:

`72^(63)=2^(189)\cdot 3^(126)`

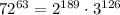
Both of these factor must be matched in the dividend in order to prove divisibility, and that indeed turns out to be true:

`2^(189)\cdot 3^(126)|2^(196)\cdot 3^(126)\implies\\2^(189)|2^(196)\,\,\mbox{and}\,\,3^(126)|3^(126)`