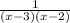Question

`\frac{x + 2}{ {x}^(2) - 9 } * \frac{x + 3}{ {x}^(2) - 4 }`
​

Answer 1

`(1)/((x-3)(x-2))`

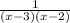
Explanation:

Factorise the denominators of both fractions

x² - 9 and x² - 4 are both differences of squares and factor as

x² - 9 = (x - 3)(x + 3) and x² - 4 = (x - 2)(x + 2), thus express as

`(x+2)/((x-3)(x+3))` ×
`(x+3)/((x-2)(x+2))`

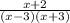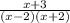
Cancel the factors (x + 3) and (x + 2) from the numerators/denominators of both fractions leaving

`(1)/((x-3)(x-2))`