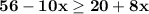
Subtract 8x on both sides.
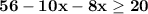
Combine −10x and −8x to get −18x.
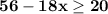
Subtract 56 from both sides.
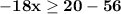
Subtract 56 from 20 to get −36.
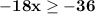
Divide both sides by −18. Since −18 is <0, the inequality direction is changed.
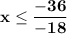
Divide −36 by −18 to get 2.
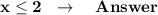
We conclude that the correct option is "C".
{ Pisces04 }