Answer:
The correct option is 2.
Explanation:
It is given that a graph of the ordered pairs formed from the corresponding terms of pattern S and pattern T.
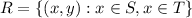
Pattern S : Starts at 10 uses the rule “subtract 1”
10, 9, 8, 7, 6, 5, 4, 3, 2, 1
Pattern T : Starts at 10 and uses the rule “subtract 2”
10, 8, 6, 4, 2, 0
The required ordered pairs are (10,10), (9,8), (8,6), (7,4), (6,2), (5,0).
In graph 1, the ordered pairs are (1,10), (3,9), (5,8), (7,7), (9,6).
In graph 2, the ordered pairs are (10,10), (9,8), (8,6), (7,4), (6,2).
In graph 3, the ordered pairs are (2,2), (4,4), (6,6), (8,8), (10,10).
Only graph 2 represents the ordered pairs formed from the corresponding terms of pattern S and pattern T.
Therefore the correct option is 2.