Question

Suppose BK is an angle bisector of △ABC. Find AB if BC=7, AK=3.5, and KC=5

Answer 1

AB = 4.9

Explanation:

Since BK is an angle bisector then the following ratios are equal

`(AB)/(BC)` =
`(AK)/(CK)`, that is

`(AB)/(7)` =
`(3.5)/(5)` ( cross- multiply )

5AB = 24.5 ( divide both sides by 5 )

AB = 4.9

Answer 2

AB=4.9

Explanation:

Given: BK is an angle bisector of △ABC and BC=7, AK=3.5, KC=5.

To find: The value of AB.

Solution:

It is given that BK is an angle bisector of △ABC, therefore by using the angle bisector theorem we have

`(AB)/(BC)=(AK)/(KC)`

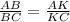
Substituting the given values, we get

`(AB)/(7)=(3.5)/(5)`

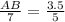
On cross multiplying, we get

`AB=\frac{3.5{*}7}{5}`

`AB=4.9`

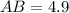
Thus, the value of AB is 4.9