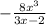Question

Simplify completely 8x^3 ÷ 6x^2 - 4x / -2x

Answer 1

`-\frac {8x^3} {3x-2}`

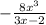
Explanation:

We are given the following expression and we are two divide these two terms:

`\frac {8x^3} {\frac {6x^2 - 4x} {-2x} }`

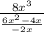
To simplify this, we will take the reciprocal of the fraction in the denominator of this expression to change it to multiplication.

`8x^3` ×
`\frac {-2x} {6x^2 - 4x}`

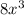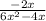
Taking the common terms out to get:

`8x^3` ×
`(-2x)/(2x(3x-2))`

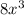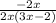
Cancelling the like terms to get:

`-(8x^3)/(3x-2)`

Answer 2

Simplified form is
`-((8x^(3))/(3x-2))`.

Explanation:

The given expression is
`8x^(3)/ (6x^(2)-4x)/(-2x)`

We can rewrite the given expression as
`= 8x^(3)* (-\frac{2x}{{6x^(2)-4x}})`

Further simplification of the expression gives
`=(-16x^(4))/(6x^(2)-4x)`

`=(-16x^(4))/(2x(3x-2))`

`=-((8x^(3))/(3x-2))`

So the simplified of the given expression is
`=[tex]-((8x^(3))/(3x-2))`