Question

The endpoints of ab are a(1,4) and b(6,-1). If point c divides ab in the ratio 2:3, the coordinates of c are ?. If point d divides ac in the ratio 3:2, the coordinates of d are ?.

Answer 1

see explanation

Explanation:

Find the coordinates of c using the section formula

`x_(c)` =
`((3(1)+(2(6))/(2+3)` =
`(3+12)/(5)` = 3

`y_(c)` =
`((3(4))+(2(-1)))/(2+3)` =
`(12-2)/(5)` = 2

coordinates of c = (3, 2)

Similarly to find the coordinates of d

`x_(d)` =
`(x(2(1))+(3(3)))/(3+2)` =
`(2+9)/(5)` =
`(11)/(5)`

`y_(d)` =
`((2(4))+(3(2)))/(3+2)` =
`(8+6)/(5)` =
`(14)/(5)`

coordinates of d = (
`(11)/(5)`,
`(14)/(5)`)

Answer 2

Answer: The co-ordinates of point C are (3, 2) and the co-ordinates of the point D are
`\left((11)/(5),(14)/(5)\right).`

Step-by-step explanation: Given that the endpoints of a line segment AB are A(1,4) and B(6,-1).

We are to find the co-ordinates of a point C that divides the line segment AB in the ratio 2 : 3.

Also, to find the co-ordinates of the point D that divides the line segment AC in the ratio 3 : 2.

We know that

the co-ordinate of a point that divides a line segment with endpoints (p. q) and (r, s) in the ratio m : n is given by

`\left((mr+np)/(m+n),(ms+nq)/(m+n)\right).`

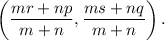
Therefore, the co-ordinates of point C will be

`C\\\\\\=\left((2* 6+3* 1)/(2+3),(2* (-1)+3* 4)/(2+3)\right)~~~~~~~~~~[\textup{here, m : n = 2 : 3}]\\\\\\=\left((12+3)/(5),(-2+12)/(5)\right)\\\\\\=\left((15)/(5),(10)/(5)\right)\\\\=(3,2).`

And, the co-ordinates of the point D will be

`D\\\\\\=\left((3* 3+2* 1)/(3+2),(3* 2+2* 4)/(3+2)\right)~~~~~~~~~~[\textup{here, m : n = 3 : 2}]\\\\\\=\left((9+2)/(5),(6+8)/(5)\right)\\\\\\=\left((11)/(5),(14)/(5)\right).`

Thus, the co-ordinates of point C are (3, 2) and the co-ordinates of the point D are
`\left((11)/(5),(14)/(5)\right).`