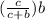Question

PLEASE HELP!!!

Rhombus ADEF is inscribed into a triangle ABC so that they share angle A and the vertex E lies on the side
BC
. What is the length of the side of the rhombus if AB=c, and AC=b.

Answer 1

Explanation:

Given that Rhombus ADEF is inscribed into a triangle ABC so that they share angle A and the vertex E lies on the side BC.Then,

AE is the angle bisector of ∠A, so divides the sides of the triangle into a proportion:

`(BE)/(CE)=(BA)/(AC)=(c)/(b)`

⇒
`(BE)/(CE)=(c)/(b)`

⇒
`(BE)/(BC)=(c)/(c+b)`

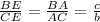
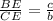
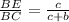
Also, ΔDBE is similar to ΔABC, then

`DE=((BE)/(BC))AC`

=
`((c)/(c+b))b`

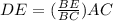
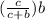
Therefore, the length of the rhombus is =
`((c)/(c+b))b`