Question

Parallelogram ABCD has vertices at A(1,2) , B(0,9) , C(7,8) , and D(8,1) . Which conclusion can be made?

1. AC⎯⎯⎯⎯⎯⊥BD⎯⎯⎯⎯⎯ ; therefore, ABCD is a rhombus.

2. AC=BD ; therefore, ABCD is a rhombus.

3. AC⎯⎯⎯⎯⎯⊥BD⎯⎯⎯⎯⎯ ; therefore, ABCD is a rectangle.

4. AC=BD ; therefore, ABCD is a rectangle.

Answer 1

Vertices of parallelogram ABCD is given as A(1,2) , B(0,9) , C(7,8) , and D(8,1) .

We will use the following analytical geometry formulas here

1. Distance between two points

`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

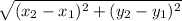
2. Slope of a line

`=(y_(2)-y_(1))/(x_(2)-x_(1))`

3. When two lines are perpendicular, product of their slopes is equal to -1.

Since ABCD is a parallelogram

1. Opposite sides are equal and parallel.

2. Diagonals bisect each other.

3. Opposite angles are equal.

Now, coming to problem

`AB=√(1^2+7^2)=√(50), BC=√(7^2+1^2)=√(50), CD=√(1^2+7^2)=√(50), DA=√(7^2+1^2)=√(50)\\\\ {\text{Slope of AB}=(7)/(-1)=-7 \\\\{\text{Slope of CB}=(1)/(-7),\\\\ {\text{Slope of CD}=(-7)/(1)=-7\\\\ {\text{Slope of AD}=(-1)/(7)`

As, you can see that, AB=BC=CD=DA=√ 50

But , slope of AB × Slope of BC =slope of CB × Slope of DC=slope of CD × Slope of DA
`=[-7 * (-1)/(7)]=1`

which is not equal to -1. It means lines which are sides of parallelogram are not perpendicular.

As, all side of parallelogram ABCD are equal, so it is a rhombus.

As, diagonal of rhombus bisect each other at right angles.

`{\text{slope of AC}} * {\text{Slope of BD}}=(6)/(6)*(-8)/(8)=-1`

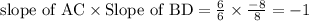
Shows that diagonals are perpendicular bisector of each other.

Option (1) : AC⊥BD; therefore, ABCD is a rhombus.

Answer 2

1. AC ⊥BD ; therefore, ABCD is a rhombus.

Explanation:

We are given,

A parallelogram ABCD with vertices A(1,2), B(0,9), C(7,8) and D(8,1).

Using Distance Formula, which gives the distance between two points (
`(x_(1),y_(1))` and (
`(x_(2),y_(2))` as
`\sqrt{(y_(2)-y_(1))^(2)+(x_(2)-x_(1))^(2)}`

So, the distance between two points are given by,

AB=
`\sqrt{(9-2)^(2)+(0-1)^(2)}=√(49+1)=√(50)` = 7.07

BC=
`\sqrt{(8-9)^(2)+(7-0)^(2)}=√(1+49)=√(50)` = 7.07

CD=
`\sqrt{(8-1)^(2)+(7-8)^(2)}=√(49+1)=√(50)` = 7.07

DA=
`\sqrt{(1-2)^(2)+(8-1)^(2)}=√(1+49)=√(50)` = 7.07

Also,

AC=
`\sqrt{(8-2)^(2)+(7-1)^(2)}=√(36+36)=√(72)` = 8.49

BD=
`\sqrt{(9-1)^(2)+(0-8)^(2)}=√(64+64)=√(138)` = 11.3

Since, we have,

AB = BC = CD = DA.

So, ABCD is a rhombus but not a rectangle.

As, AC ≠ BD. Moreover, two diagonals are perpendicular to each other in a rhombus. Thus, AC ⊥ BD.

Hence, we get that, Option A is correct.