Question

A 0.180-kilogram car traveling at 0.80 m/s to the right collides with a 0.100-kilogram cart intially at rest. The carts lock together upon collison. Calculate the final velocity of the carts

Answer 1

0.51 m/s to the right.

Step-by-step explanation

The two carts lock together. As a result, the collision is inelastic. Kinetic energy will not conserve. Still, momentum conserves.

What's the momentum p of the two carts?

Before the collisions:

• 
  `p_1 = m_1 \cdot v_1 = 0.180 * 0.80 = 0.144 \; \text{kg} \cdot \text{m}\cdot \text{s}^(-1)`;
• 
  `p_2 = m_2 \cdot v_2 = 0`.

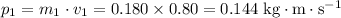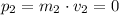• Sum of momentum:
  `p = p_1 + p_2 = 0.144\; \text{kg} \cdot \text{m}\cdot \text{s}^(-1)`.

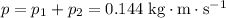Momentum conserves. As a result,
`p(\text{after collision}) = p(\text{before collision}) = 0.144 \; \text{kg} \cdot \text{m}\cdot \text{s}^(-1)`

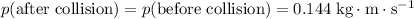
Velocity is the same for the two carts after the collision. Let
`v` denote that velocity.

`p(\text{after collision}) = m_1\cdot v+ m_2 \cdot v = (m_1 + m_2) \cdot v`.

`v = \frac{p(\text{after collision})}{m_1 + m_2} \\ \phantom{v} = (0.144)/(0.180 + 0.100) \\ \phantom{v} = 0.51 \; \text{m}\cdot \text{s}^(-1)`.

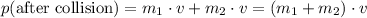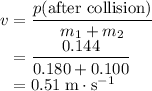Direction of the movement will stay the same. Both cars are now moving to the right.