Answer:
The average rate of change of f(x) from 1 to 4 is -80.
Explanation:
The average rate of change of f(x) from a to b is defined as
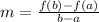
The average rate of change of f(x) from 1 to 4 is defined as
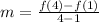
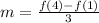
From the given table it is clear that the the value of the function is 244 at x=4 and 484 at x=1. So f(4)=244 and f(1)=484. Put these values in the above equation.
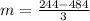
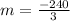
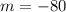
Therefore the average rate of change of f(x) from 1 to 4 is -80.