Question

By letting y = x^1/3, or otherwise, find the values of x for which x^1/3 -2x^-1/3 = 1

Answer 1

In this case, the problem is asking us to solve the equation

`x^{(1)/(3)} - \frac{2}{x^{(1)/(3)}} = 1`

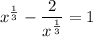
by substituting
`y = x^{(1)/(3)}`.

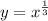First, let's substitute the variable into the original equation:

`y - (2)/(y) = 1`

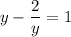
Now, let's solve:

`y - (2)/(y) = 1`

• Set up

`y\Bigg(y - (2)/(y)\Bigg) = y(1) \Rightarrow y^2 - 2 = y`

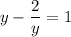
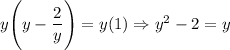
• Multiply the entire equation by
  `y` to remove the fraction over
  `y`

`y^2 - y - 2 = 0`

• Subtract
  `y` from both sides of the equation for easier factoring

`(y - 2)(y + 1) = 0`

• Factor

`y - 2 = 0 \,\, \textrm{and} \,\, y + 1 = 0`

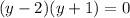
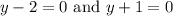
• Solve the factored equation using the Zero Product Property

`y = 2, -1`

• Solve each equation

Now, we aren't done yet. We have to find our answer in terms of the original variable,
`x`. To do this, set each value for
`y` into the substitution equation we found earlier,
`y = x^{(1)/(3)}`:

`2 = x^{(1)/(3)}`

`2^3 = x`

`x = 8`

`-1 = x^{(1)/(3)}`

`(-1)^3 = x`

`x = -1`

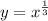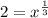
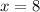
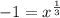
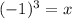
The solutions for the equation are x = -1, 8.