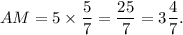Question

Given: △ACM, m∠C=90°, CP ⊥ AM

AC:CM=3:4, MP-AP=1.


Find AM. PLEASE HELP! DUE IN AN HOUR AND I HAVE NO IDEA!

Answer 1

Answer: The answer is
`3(4)/(7).`

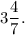
Step-by-step explanation: Given in the question that ΔAM is a right-angled triangle, where ∠C = 90°, CP ⊥ AM, AC : CM = 3 : 4 and MP - AP = 1. We are to find AM.

Let, AC = 3x and CM = 4x.

In the right-angled triangle ACM, we have

`AM^2=AC^2+CM^2=(3x)^2+(4x)^2=9x^2+16x^2=25x^2\\\\\Rightarrow AM=5x.`

Now,

`AM=AP+PM=AP+(AP+1)\\\\\Rightarrow 2AP=AM-1\\\\\Rightarrow 2AP=5x-1.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(A)`

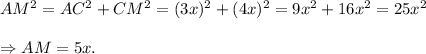
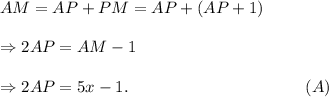
Now, since CP ⊥ AM, so ΔACP and ΔMCP are both right-angled triangles.

So,

`CP^2=AC^2-AP^2=CM^2-MP^2\\\\\Rightarrow (3x)^2-AP^2=(4x)^2-(AP+1)^2\\\\\Rightarrow 9x^2-AP^2=16x^2-AP^2-2AP-1\\\\\Rightarrow 2AP=7x^2-1.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(B)`

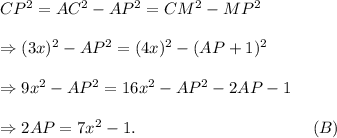
Comparing equations (A) and (B), we have

`5x-1=7x^2-1\\\\\Rightarrow 5x=7x^2\\\\\Rightarrow x=(5)/(7),~\textup{since }x\\eq 0.`

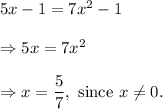
Thus,

`AM=5*(5)/(7)=(25)/(7)=3(4)/(7).`