Answer:
Inequality representing the situation is
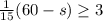 i.e.
i.e.
 .
.
Explanation:
Let the number of days = s
Since, she has to work for 60 days and skipped for s days.
The number of days she worked = 60 - s
As, she worked at a rate of
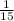 part of a blanket.
part of a blanket.
So, she worked at
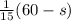 days in total.
days in total.
Since, she has to make minimum of 3 blankets, we get the inequality,
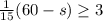
i.e.
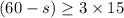
i.e.
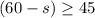
i.e.
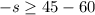
i.e.

i.e.

So, she can skip the days less than 15 and still meet her goal.
Hence, the inequality representing the situation is
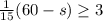 i.e.
i.e.
 .
.
The solution plotted is given below.