Question

GEOMETRY PLZ HELP

The figure shows three right triangles. Triangles ABD, CAD, and CBA are similar. Theorem: If two triangles are similar, the corresponding sides are in proportion. Using the given theorem, which two statements help to prove that if segment BC is x, then x2 = 74?
Here is the picture
A Segment BC • segment DC = 49
Segment BC • segment BD = 35

B Segment BC • segment DC = 49
Segment BC • segment BD = 25

C Segment BC • segment DC = 25
Segment BC • segment BD = 35

D Segment BC • segment DC = 25
Segment BC • segment BD = 49

Answer 1

B- Segment BC ⋅ segment DC = 49

Segment BC ⋅ segment BD = 25

Explanation:

I took the test and it was correct

Answer 2

Option B is true

Explanation:

We are given that three right triangles .Triangles ABD,CAD and CBA are similar.

When two triangles are similar then, the corresponding sidea are in equal proportion.

We have AB=5 units

AC= 7 units

BC=x

Triangles ABD is similar triangle CBA

`(AB)/(BD)=(BC)/(AB)`

`AB^2=BC\cdot BD`

`(5)^2=BC\cdot BD`

`BC\cdot BD=25`

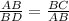
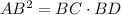
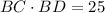
When triangle CAD and CBA are similar

Then,
`(AC)/(BC)=(CD)/(AC)`

`AC^2=CD\cdot BC`

`(7)^2=CD\cdot BC`

`49=CD\cdot BC`

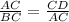
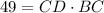
In traingle CBA, uisng pythagoras theorem

`AB^2+AC^2=BC^2`

`BC\cdot BD+BC\cdot CD=x^2`

`25+49=x^2`

`x^2=74`

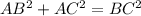
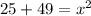
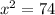
Hence, option B is true.