Question

Trey drove to the mountains last weekend. There was heavy traffic on the way there, and the trip 8 took hours. When Trey drove home, there was no traffic and the trip only took 6 hours. If his average rate was 16 miles per hour faster on the trip home, how far away does Trey live from the mountains?

Answer 1

Trey lives 384 feet.

Explanation:

Let the average rate be represented by s, and the distance by d.

speed =
`(distance)/(time)`

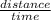
⇒ distance = speed x time

i.e d = s x t

On his first trip,

d = s x 8

d = 8s ............ 1

on his trip home, the average rate was 16 miles per hour faster, so that;

d = (s + 16) x 6

d = 6s + 96 ............ 2

Equation 1 and 2, we have;

8s = 6s + 96

8s - 6s = 96

2s = 96

s = 48

The average rate is 48 miles per hour.

Thus from equation 1 (also equation 2 can be used),

d = 48 x 8

= 384

Therefore, Trey lives 384 feet from the mountains.