Answer:
The equation of the line that passes through the given points is:
Hence, option D is correct.
The graph of the line equation is also attached below.
Explanation:
Given the points
Finding the slope between (-5, 10) and (5, -10)
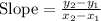
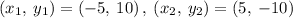
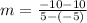
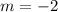
Using the point-slope form to determine the line equation
Point slope form:
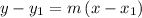
where m is the slope of the line and (x₁, y₁) is the point
substituting the values m = -2 and the point (-5, 10)
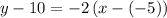

Add 10 to both sides
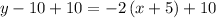
simplify
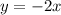
Thus, the equation of the line that passes through the given points is:
Hence, option D is correct.
The graph of the line equation is also attached below.