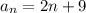Question

Write a recursive formula and an explicit formula for the following arithmetic sequence.

11, 13, 15, 17, 19, ...
A recursive formula is a = INan=.
(Simplify your answers.)
An explicit formula is an =
(Simplify your answer.)

Answer 1

The recursive formula for the given arithmetic sequence is a_n = a_(n-1) + 2 for n ≥ 2, where a_1 = 11.

The explicit formula is a_n = 2n + 9.

Step-by-step explanation:

The arithmetic sequence provided is 11, 13, 15, 17, 19, ... where the common difference (d) is 2, since each term increases by 2 from the previous term.

A recursive formula for an arithmetic sequence specifies each term as a function of its preceding term. The recursive formula for the given sequence is:

an = an-1 + d for n ≥ 2,
where a1 = 11 and d = 2.

An explicit formula, on the other hand, calculates any term directly based on its position in the sequence. The explicit formula for this sequence is:

an = a1 + (n - 1)d,
which simplifies to an = 11 + (n - 1) × 2, or an = 2n + 9.

Answer 2

Please check the explanation.

Step-by-step explanation:

Given the sequence

11, 13, 15, 17, 19, ...

Determining the Recursive formula:

We know that a recursive formula is termed as a formula that specifies each term of the given sequence using the preceding terms.

From the given sequence it is clear that every term can be obtained by adding two to the previous term.

i.e. 13 = 11+2, 15 = 13+2, 17 = 15+2, 19 = 17+2

so

aₙ₊₁ = aₙ+2, for n ≥1

Therefore, a recursive formula is:

• aₙ₊₁ = aₙ+2, for n ≥1

Determining the Explicit formula:

Given the sequence

11, 13, 15, 17, 19, ...

An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

computing the differences of all the adjacent terms

`3-11=2,\:\quad \:15-13=2,\:\quad \:17-15=2,\:\quad \:19-17=2`

The difference between all the adjacent terms is the same and equal to

`d=2`

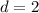
also

`a_1=11`

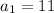
so substituting
`d=2`,
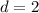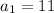`a_1=11` in the nth terms

`a_n=a_1+\left(n-1\right)d`

`a_n=2\left(n-1\right)+11`

`a_n=2n+9`

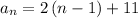
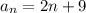
Therefore, the Explicit formula is:

`a_n=2n+9`