Question

Calculate the force exerted on the pipe by A and B respectively.

Answer 1

Taking
`g = 10 \; \text{N}\cdot \text{kg}^(-1)`.

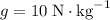• Worker A: 476 N.
• Worker B: 324 N.

Step-by-step explanation

Worker A:

Consider the pipe as a level. Worker A will supply the effort, and worker B will act as the fulcrum.

• Worker A applies an upward force 4.2 meters away from the fulcrum.

• The weight of the pipe acts at the center of its mass, which is 2.5 meters away from the fulcrum. The level is class two.

`4.2 * F_\text{A} = 2.5 * m\cdot g\\`

`F_\text{A} = (2.5)/(4.2) \; m\cdot g\\\phantom{F_\text{A}} = (2.5)/(4.2) * 80 * 10\\\phantom{F_\text{A}} = 476 \; \text{N}`

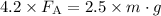
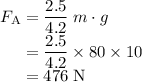
Worker B:

Again, consider the pipe as a level. Worker B will now supply the effort, and worker A will act as the fulcrum.

• Worker B applied an upward force
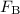  `F_\text{B}` 4.2 meters away on the left-hand side of the fulcrum.

The weight of the pipe acts at two positions.

• 
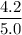  `(4.2)/(5.0)` of the pipe's mass acts downwards between worker A and B. That
  `(4.2)/(5.0) * 80 \; \text{kg}` of mass will act downward at its center of mass
  `(1)/(2) * 4.2\;\text{m}` away on the left-hand side of the fulcrum.
  `F_\text{1} = (4.2)/(5.0) * 80 * 10 = 672 \; \text{N}`
• 
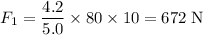
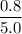  `(0.8)/(5.0)` of the pipe's mass acts downwards to the right of worker B. That
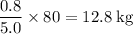  `(0.8)/(5.0) * 80 = 12.8 \; \text{kg}` of mass will act also downward at its center of mass
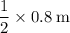  `(1)/(2) * 0.8\;\text{m}` away on the right-hand side of the fulcrum.
  `F_\text{2} = (0.8)/(5.0) * 80 * 10 = 128 \; \text{N}`

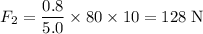
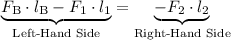`\underbrace{F_\text{B} \cdot l_\text{B} - F_(1) \cdot l_(1)}_{\text{Left-Hand Side}} =\underbrace{-F_(2) \cdot l_(2)}_{\text{Right-Hand Side}}` for the pipe to balance. Therefore:

`F_\text{B} = \frac{F_(1) \cdot l_(1) - F_(2) \cdot l_(2)}{l_\text{B}} \; \\\phantom{F_\text{B}} = (672 * (4.2)/(2) - 128 * (0.8)/(2))/(4.2) \\\phantom{F_\text{B}} = 324\; \text{N}`.

Make sure that
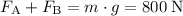`F_\text{A} + F_\text{B}= m \cdot g = 800 \; \text{N}`.