Question

A bag contains six real diamonds and five fake diamonds. If six diamonds are picked from the bag at random, what is the probability that at most four of them are real?

Answer 1

Answer: The answer is 77% (approximately).

Step-by-step explanation: Given that a bag contains 11 diamonds, out of which 6 are real and 5 are fake. 6 diamonds are picked from the bag randomly. We are to calculate the probability that at most four of the 6 diamonds are real.

Since we can choose at most 4 real diamonds, so the number of ways in which we can do so is given by

`n=(5!)/(5!0!)* (6!)/(1!5!)+(5!)/(4!1!)* (6!)/(2!4!)+(5!)/(3!2!)* (6!)/(3!3!)+(5!)/(4!1!)* (6!)/(4!2!)\\\\\\\Rightarrow n=1*6+5* 15+10*20+5* 15\\\\\Rightarrow n=6+75+200+75\\\\\Rightarrow n=356.`

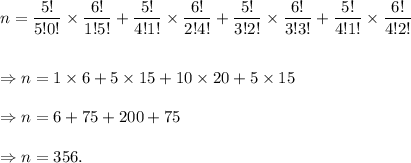
And the total number of ways in which we can choose 6 diamonds out of 11 is

`N=(11!)/(6!5!)=462.`

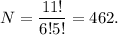
Therefore, the required probability will be

`p=(n)/(N)=(356)/(462)\sim .77=77\%.`

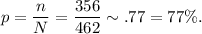
Thus, the probability is 77% approx.