Question

A population of fish in a lake is 14000 in 2010. The population decreases 6% annually. What is the population in 2019

Answer 1

8022.

Explanation:

Let x be the number of years after 2010.

We have been given a population of fish in a lake is 14000 in 2010. The population decreases 6% annually.

We can see that population of fish is the lake is decreasing exponentially as it is decreasing 6% annually.

Since we know that an exponential function is in form:
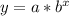`y=a*b^x`, where,

a = Initial value,

b = For decrease or decay b is in form (1-r) where r represents decay rate in decimal form.

Let us convert our given decay rate in decimal form.

`6\5=(6)/(100)=0.06`

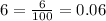
Upon substituting our given values in exponential form of function we will get the population of fish in the lake after x years as:

`y=14,000*(1-0.06)^x`

`y=14,000*(0.94)^x`

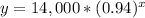
Let us find x by subtracting 2010 from 2019.

`x=2019-2010=9`

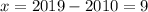
Upon substituting x=9 in our function we will get,

`y=14,000*(0.94)^9`

`y=14,000*0.5729948022286167`

`y=8021.927\approx 8022`

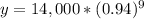
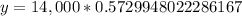
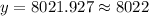
Therefore, the population of fish in 2019 will be 8022.