Question

use the matrix tool to solve the system of equations choose the correct ordered pair4x-y=10 and 8x+5y=34

Answer 1

`\left[\begin{array}{ccc}x\\y\\\end{array}\right] = \left[\begin{array}{ccc}3\\2\\\end{array}\right]`

Solution of the given system of equations

x = 3 and y= 2

Explanation:

Step(i):-

Given system of equations are

4x - y = 10 ...(i)

8x +5y = 34...(ii)

The matrix form

A X = B

`\left[\begin{array}{ccc}4&-1\\8&5\\\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right] = \left[\begin{array}{ccc}10\\34\\\end{array}\right]`

Step(ii):-

By using matrix inversion method

`A^(-1) = (1)/(|A|) adj A`

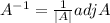
|A| = ad-b c = 4(5) - 8(-1) = 20+8 = 28

Given matrix

`A = \left[\begin{array}{ccc}4&-1\\8&5\\\end{array}\right]`

`AdjA = \left[\begin{array}{ccc}d&-b\\-c&a\\\end{array}\right]`

`A djA = \left[\begin{array}{ccc}5&1\\-8&4\\\end{array}\right]`

Inverse of the matrix

`A^(-1) = (1)/(|A|) adj A`

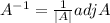
`A^(-1) = (1)/(|A|) A djA =(1)/(28) \left[\begin{array}{ccc}5&1\\-8&4\\\end{array}\right]`

Step(iii):-

The solution of the given system of equations by using matrix inversion method

X = A⁻¹ B

`X = A^(-1)B =(1)/(28) \left[\begin{array}{ccc}5&1\\-8&4\\\end{array}\right]\left[\begin{array}{ccc}10\\34\\\end{array}\right]`

`X = A^(-1)B =(1)/(28) \left[\begin{array}{ccc}5X10+1X34\\-8X10+4X34\\\end{array}\right]`

`\left[\begin{array}{ccc}x\\y\\\end{array}\right] =(1)/(28) \left[\begin{array}{ccc}84\\56\\\end{array}\right]`

`\left[\begin{array}{ccc}x\\y\\\end{array}\right] = \left[\begin{array}{ccc}3\\2\\\end{array}\right]`

Final answer:-

Solution of the given system x = 3 and y= 2