Answer:
Explanation:
Given: △KOE∼△LSV, OT and SP are angle bisectors that is ∠KOT=∠TOE and ∠LSP=∠PSV.
To Prove:
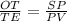
Proof: Since, OT and SP are angle bisectors that is ∠KOT=∠TOE and ∠LSP=∠PSV, and ∠KOE=∠LSV (given).Therefore, ∠TOE=∠PSV (1)
Consider △OTE and △PSV,
∠E = ∠V (△KOE∼△LSV)
∠TOE=∠PSV(From (1)
Thus, by AA similarity, △OTE is similar to △PSV, therefore using similarity condition,
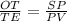
Hence proved.