Answer:
option (a) is correct.
the value of line segment DC is 19 .
Explanation:
Given a trapezoid ABCD with AB║DC and AB = 13 , GH = 16
We have to find the length of DC.
mid segment is a line joining mid points of two non parallel sides of a trapezoid.
Trapezoid mid segment theorem states that the mid segment of a trapezoid is equal to half of sum of its two parallel sides.
Since, G is mid point of side AD as AG = GD (given)
also, H is mid point of side BC as BH = HC (given)
Thus, GH is the mid segment of the trapezoid ABCD.
AB║DC , GH ║DC AB║GH
Thus, using trapezoid mid segment theorem, we have

Substitute known values,
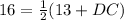
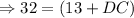

Thus, the value of line segment DC is 19 .
Hence, option (a) is correct.