Answer:
10 miles.
Explanation:
Let x be the number of miles on Henry's longest race.
We have been given that Henry ran five races, each of which was a different positive integer number of miles.
We can set an equation for the average of races as:
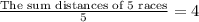
As distance covered in each race is a different positive integer, so let his first four races be 1, 2, 3, 4.
Now let us substitute the distances of 5 races as:
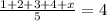
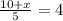
Let us multiply both sides of our equation by 5.
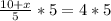
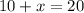
Let us subtract 10 from both sides of our equation.
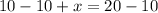
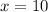
Therefore, the maximum possible distance of Henry's longest race is 10 miles.