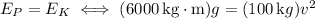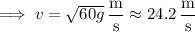Assuming it starts at rest, the roller coaster only has potential energy at the top of the hill, which is
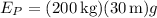
When it reaches the bottom, its potential energy will have converted to kinetic energy,
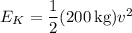
where
 is its velocity at that point. By the law of conservation of energy, assuming no loss of energy due to other sources (e.g. sound, heat), we have
is its velocity at that point. By the law of conservation of energy, assuming no loss of energy due to other sources (e.g. sound, heat), we have