Question

A right triangle has side lengths that are consecutive integers and a perimeter of 12 feet what are the angles of the triangle

Answer 1

The simplest right triangle is a 3-4-5 triangle which happens to add to 12.

So tangent of 4/3 = 1.33 or theta = 53.06 deg.

Also sin 4/5 = .8 and theta = 53.1 deg.

The other acute angle must be 180 - 90 - 53.5 = 36.5 deg.

Also tan 3/4 = .75 or theta = 36.9 deg for the other angle.

Explanation:

Answer 2

Angles of the triangle are 90°, 50.77° and 39.23°.

Explanation:

Let the smallest side be x. Given that other sides are consecutive integers. So other sides are x+1 and x+2.

We have perimeter = 12 feet

So, x + x + 1 + x + 2 = 12

3x + 3 = 12

x = 3 feet

So the sides of the triangle are 3, 4 and 5 feet.

We have cosine formula

cosC
`=\sqrt{(a^2+b^2-c^2)/(2ab)}`

Consider a = 3 , b = 4 and c = 5

cosC
`=\sqrt{(3^2+4^2-5^2)/(2*3*4)}=0`

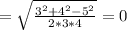
∠C = 90°

Similarly

cosB
`=\sqrt{(3^2+5^2-4^2)/(2*3*5)}=0.775`

∠B = 39.23°

∠A = 180-(90+39.23) = 50.77°

Angles of the triangle are 90°, 50.77° and 39.23°.