Answer:
(A)
Explanation:
The given trigonometric ratio is :
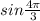
On solving this, we get
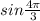
=
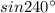
=
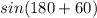
=
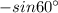
=
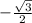
(A) The given trigonometric ratio is :
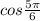
=
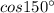
=
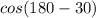
=
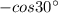
=
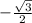
Which is equivalent to the given trigonometric ratio, thus (A) is correct.
(B) The given trigonometric ratio is :
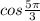
=
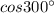
=
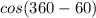
=
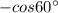
=
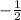
which is not equivalent to the given trigonometric ratio, thus(B) is incorrect.
(C) The given trigonometric ratio is :
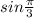
=

which is not equivalent to the given trigonometric ratio, thus(C) is incorrect.
(D) The given trigonometric ratio is :
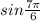
=
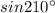
=
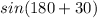
=
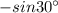
=
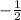
which is not equivalent to the given trigonometric ratio, thus(D) is incorrect.