Question

Point x is at 2/3 on number line. On the same number line point y is the same distance from 0 as point x but has a numberator of 8 whay is the denominator line to model the problem

Answer 1

Answer: The answer is 12.

Step-by-step explanation: Given that a point 'x' is lying at
`(2)/(3)` on the number line. Another point 'y' is also lying at the same distance from 0 but has a numerator of 8. We are to find the denominator of 'y'.

Since 'x' is lying at
`(2)/(3)` on the number line so its distance from 0 will be

`d_x=(2)/(3)-0=(2)/(3).`

Let the denominator of 'y' be p, then its distance from 0 will be

`d_y=(8)/(p)-0=(8)/(p).`

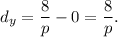
According to the given information, we must have

`d_x=d_y\\\\\\\Rightarrow (2)/(3)=(8)/(p)\\\\\\\Rightarrow p=(8* 3)/(2)=12.`

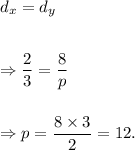
Thus, the denominator will be 12.