Question

A helicopter flying 3590 feet above ground spots the top of a 150-foot y'all cell phone tower at an angle of depression of 77° how far must the helpicopter fly to be directly over the tower

Answer 1

794.19 feet.

Explanation:

Please find the attachment.

Let x be the distance helicopter needs to fly to be directly over the tower.

We have been given that a helicopter flying 3590 feet above ground spots the top of a 150-foot y'all cell phone tower at an angle of depression of 77°.

We can see from our attachment that helicopter, tower and angle of depression forms a right triangle.

As height of tower is 150 feet, so the vertical distance between helicopter and tower will be
`3590-150=3440` feet.

We cab see from our attachment that the side with length 3590-150 feet is opposite and side x is adjacent side to 77 degree angle.

Since we know that tangent relates the opposite side of a right triangle to its adjacent side, so we will use tangent to find the length of x.

`\text{Tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

Upon substituting our given values in above formula we will get,

`\text{Tan}(77^o)=(3590-150)/(x)`

`\text{Tan}(77^o)=(3440)/(x)`

`x=\frac{3440}{\text{Tan}(77^o)}`

`x=(3440)/(4.331475874284)`

`x=794.1865\approx 794.19`

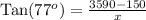
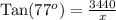
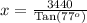
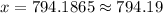
Therefore, the helicopter must fly approximately 794.19 feet to be directly over the tower.