Question

What is the sum of the first seven terms of the geometric series 2 − 8 + 32 − . . . ?

Hint: cap s sub n equals start fraction a sub one left parenthesis one minus r to the power of n end power right parenthesis over one minus r end fraction comma r ≠ 1, where a1 is the first term and r is the common ratio.

S7 = 6,554
S7 = −8,192
S7 = 8,192
S7 = 10,922

Answer 1

`S_7=6554`

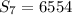
Explanation:

The given series is
`2-8+32-...`

The first term of the sequence is

`a_1=2`

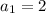
There is a common ratio of

`r=-4`

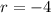
The sum of the first n terms of a geometric sequence is given by the formula;

`S_n=(a_1(1-r^n))/(1-r)`

We want to find the first seven terms so
`n=7`

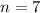
We substitute the given values into the formula to obtain;

`S_7=(2(1-(-4)^7))/(1--4)`

`S_7=(2(1--16384))/(1--4)`

`S_7=(2(16385))/(5)`

`S_7=2(3277)`

`S_7=6554`

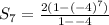
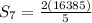
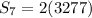
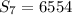
The correct answer is A