Question

a town has 685 households. the number of people per household is normally distributed with the mean of 3.67 and the standard deviation of 0.34. approximately how many households have between 2.99 and 4.01

Answer 1

560 households.

Explanation:

We have been given that a town has 685 households. the number of people per household is normally distributed with the mean of 3.67 and the standard deviation of 0.34.

Let us find z-score corresponding to sample scores, 2.99 and 4.01, using z-score formula.

`z=(x-\mu)/(\sigma)`, where,

`z=\text{z-score}`,

`x=\text{Sample score}`,

`\mu=\text{Mean}`,

`\sigma=\text{Standard deviation}`.

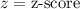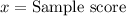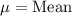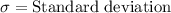Let us find z-score for sample score 2.99.

`z=(2.99-3.67)/(0.34)`

`z=(-0.68)/(0.34)`

`z=-2`

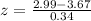
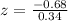
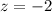
Let us find z-core for sample score 4.01.

`z=(4.01-3.67)/(0.34)`

`z=(0.34)/(0.34)`

`z=1`

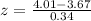
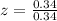
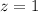
Now let us find probability of z-score greater than -2 and z-score less than 1.

We will use formula:
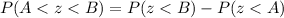`P(A<z<B)=P(z<B)-P(z<A)` to solve our problem.

`P(-2<z<1)=P(z<1)-P(z<-2)`

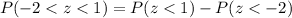
Using normal distribution table we will get,

`P(-2<z<1)=0.84134 -0.02275`

`P(-2<z<1)=0.81859`

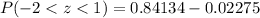
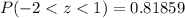
So, the probability of house holds between 2.99 and 4.01 is 0.81859. To find the number of households between 2.99 and 4.01, we will multiply our probability by total number of households.

`\text{Number of households between 2.99 and 4.01}=0.81859* 685`

`\text{Number of households between 2.99 and 4.01}=560.73415\approx 560`

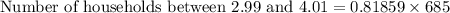
Therefore, approximately 560 households have between 2.99 and 4.01.