Answer:
Option a.
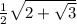
Explanation:
In this question we have to find out the exact value of cos 15 by half angle identity.
As we know that
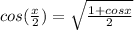 is the half angle identity.
is the half angle identity.
From half this identity we can write cos15 as
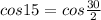 =
=
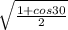
cos 15 =
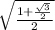
=
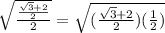
=
/(2) \sqrt{2+√(3) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jpsc591inehu2qa1ub2i5763iw3lkomcy7.png)
So Option a.
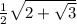 is the right option.
is the right option.