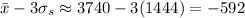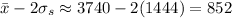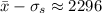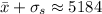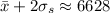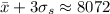1 Answer

EdSF · Answer 1 · 2020-01-06T16:57:28+0000

The mean you found is correct, but the standard deviation is not. Recall that the standard deviation
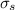$\sigma_s$ (
for sample) of
points is given by

$\sigma_s=\sqrt{\frac1{n-1}\displaystyle\sum_(1\le i\le n)(x_i-\bar x)^2}$

where
n=10 is the sample size,
$\bar x=3740$ is the sample mean, and
x_i are the prices listed in the circled column. So

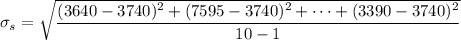
$\sigma_s=\sqrt{((3640-3740)^2+(7595-3740)^2+\cdots+(3390-3740)^2)/(10-1)}$

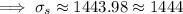
$\implies\sigma_s\approx1443.98\approx1444$

I can't tell if you need to provide any more info beyond this, but given there's a plot of a generalized bell curve, I think you're also supposed to label the plot.

At the center of the bell-shaped/normal distribution is the mean. Notice there are three tick marks to either side of the mean - these are probably supposed to represent prices that fall exactly 1, 2, and 3 standard deviations from the mean. These are, from left to right,

$\bar x-3\sigma_s\approx3740-3(1444)=-592$