Answer:
1)
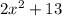
2) Option C.
3) Option B.
Explanation:
1. You must apply the Distributive property as following:
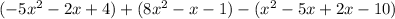
2. Now, you must distribute the negative sign, then you have:
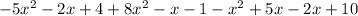
3. Finally, you must add the like terms. Then you obtain the polynomial:
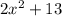
4. By definition, a polynomial that has two terms is classified as a binomial. Therefore, the answer is the option C.
5. The degree of a polynomial is determined by highest exponent of the variable. So, it is a polynomial of degree 2 (option B).