Answer:
The function g(x) is defined as
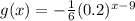 .
.
Explanation:
The given function is
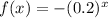
The function f(x) transformed 9 units right, compressed vertically by factor of 1/6 and reflected across the x-axis.
The transformation of function is defined as
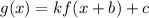
Where, k is vertical stretch, b is horizontal shift and c is vertical shift.
If b>0, then the graph of f(x) shifts b units left and if b>0, then the graph of f(x) shifts b units right.
If c>0, then the graph of f(x) shifts c units upward and if c>0, then the graph of f(x) shifts c units downward.
The value of b is -9 because the graph shifts 9 units right. The value of k is 1/6. If the graph of function f(x)reflect across x-axis, therefore the function is defined as -f(x).
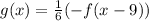
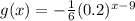
![[\because f(x)=-(0.2)^x]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/in6vtj4jfrmp0qn8pec58tsyohkbpk7egu.png)
Therefore the function g(x) is defined as
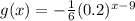 .
.