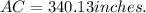Question

A utility worker is installing a 25-foot pole AB at the foot of a hill. Two guy wires, AC and AD, will help keep the pole vertical. A. To the nearest inch, how long should AC be? B. AD is perpendicular to the hill, which makes an angle of 28 with a horizontal line. To the nearest inch, how long should this guy wire be?

Answer 1

Explanation:

Since, AB is the vertical pole, then the guy wires AC and AD will be inclined at equal angles to keep the pole stand vertical. therefore, ∠CAB=∠BAD.

From ΔABD, we have

∠ABD+∠BAD+∠ADB=180° (Angle sum property)

⇒62°+∠BAD+90°=180°

⇒∠BAD=180-152

⇒∠BAD=28°

Thus, using trigonometry in ΔABD,

`(AD)/(AB)=sin62^(\circ)`

⇒
`(AD)/(300)=0.882`

⇒
`AD=264.88 inches`

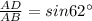
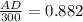
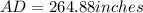
Now, ∠CAB=∠BAD=28°

From ΔCAB, we have

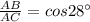
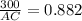
`(AB)/(AC)=cos28^(\circ)`

⇒
`(300)/(AC)=0.882`

⇒
`AC=340.13 inches.`